lunes, 25 de abril de 2011

MATEMATICAS

De Wikipedia, la enciclopedia libre
Euclides, matemático griego, del siglo III a. C., tal como fue imaginado por Rafael. Detalle de La Escuela de Atenas.[1]
Las matemáticas o la matemática (del lat. mathematĭca, y éste del gr. μαθηματικά, derivado de μάθημα, conocimiento) es una ciencia que, partiendo de axiomas y siguiendo el razonamiento lógico, estudia las propiedades y relaciones cuantitativas entre los entes abstractos (números, figuras geométricas, símbolos).[2] Mediante las matemáticas conocemos las cantidades, las estructuras, el espacio y los cambios. Los matemáticos buscan patrones,[3] [4] formulan nuevas conjeturas e intentan alcanzar la verdad matemática mediante rigurosas deducciones. Éstas les permiten establecer los axiomas y las definiciones apropiados para dicho fin.[5]
Existe cierto debate acerca de si los objetos matemáticos, como los números y puntos, realmente existen o si provienen de la imaginación humana. El matemático Benjamin Peirce definió las matemáticas como "la ciencia que señala las conclusiones necesarias".[6] Por otro lado, Albert Einstein declaró que "cuando las leyes de la matemática se refieren a la realidad, no son ciertas; cuando son ciertas, no se refieren a la realidad".[7]
Mediante la abstracción y el uso de la lógica en el razonamiento, las matemáticas han evolucionado basándose en las cuentas, el cálculo y las mediciones, junto con el estudio sistemático de la forma y el movimiento de los objetos físicos. Las matemáticas, desde sus comienzos, han tenido un fin práctico (véase: Historia de la matemática). Las explicaciones que se apoyaban en la lógica aparecieron por primera vez con la matemática helénica, especialmente con los Elementos de Euclides. Las matemáticas siguieron desarrollándose, con continuas interrupciones, hasta que en el Renacimiento las innovaciones matemáticas interactuaron con los nuevos descubrimientos científicos. Como consecuencia, hubo una aceleración en la investigación que continúa hasta la actualidad.
Hoy en día, las Matemáticas se usan en todo el mundo como una herramienta esencial en muchos campos, entre los que se encuentran las ciencias naturales, la ingeniería, la medicina y las ciencias sociales, e incluso disciplinas que, aparentemente, no están vinculadas con ella, como la música (por ejemplo, en cuestiones de resonancia armónica). Las matemáticas aplicadas, rama de las matemáticas destinada a la aplicación de los conocimientos matemáticos a otros ámbitos, inspiran y hacen uso de los nuevos descubrimientos matemáticos y, en ocasiones, conducen al desarrollo de nuevas disciplinas. Los matemáticos también participan en las matemáticas puras, sin tener en cuenta la aplicación de esta ciencia, aunque las aplicaciones prácticas de las matemáticas puras suelen ser descubiertas con el paso del tiempo.[8]

Contenido

[ocultar]

[editar] Etimología

La palabra "matemática" (del griego μαθηματικά, «lo que se aprende») viene del griego antiguo μάθημα (máthēma), que quiere decir «campo de estudio o instrucción». El significado se contrapone a μουσική (musiké) «lo que se puede entender sin haber sido instruido», que refiere a poesía, retórica y campos similares, mientras que μαθηματική se refiere a las áreas del conocimiento que sólo pueden entenderse tras haber sido instruido en las mismas (astronomía, aritmética).[9] Aunque el término ya era usado por los pitagóricos en el siglo VI a. C., alcanzó su significado más técnico y reducido de "estudio matemático" en los tiempos de Aristóteles (siglo IV a. C.). Su adjetivo es μαθηματικός (mathēmatikós), "relacionado con el aprendizaje", lo cual, de manera similar, vino a significar "matemático". En particular, μαθηματική τέχνη (mathēmatikḗ tékhnē; en latín ars mathematica), significa "el arte matemática".
La forma plural matemáticas viene de la forma latina mathematica (Cicerón), basada en el plural en griego τα μαθηματικά (ta mathēmatiká), usada por Aristóteles y que significa, a grandes rasgos, "todas las cosas matemáticas".

[editar] Historia

Artículo principal: Historia de la matemática
Instrumentos para cálculos matemáticos
Antiguos
Ábaco
Ábaco de Napier
Regla de cálculo
Regla y compás
Cálculo mental
Nuevos
Calculadoras
Ordenadores:
(Lenguajes de programación
software especializado)
La evolución de la matemática puede ser considerada como el resultado de un incremento de la capacidad de abstracción del hombre o como una expansión de la materia estudiada. Los primeros conceptos abstractos utilizados por el hombre, aunque también por muchos animales,[10] fueron probablemente los números. Esta noción nació de la necesidad de contar los objetos que nos rodeaban.
Desde el comienzo de la historia, las principales disciplinas matemáticas surgieron de la necesidad del hombre de hacer cálculos con el fin de controlar los impuestos y el comercio, comprender las relaciones entre los números, la medición de terrenos y la predicción de los eventos astronómicos. Estas necesidades están estrechamente relacionadas con las principales propiedades que estudian las matemáticas — la cantidad, la estructura, el espacio y el cambio. Desde entonces, las matemáticas han tenido un profuso desarrollo y se ha producido una fructífera interacción entre las matemáticas y la ciencia, en beneficio de ambas. Diversos descubrimientos matemáticos se han sucedido a lo largo de la historia y se continúan produciendo en la actualidad.
Además de saber contar los objetos físicos, los hombres prehistóricos también sabían cómo contar cantidades abstractas como el tiempo (días, estaciones, años, etc.) Asimismo empezaron a dominar la aritmética elemental (suma, resta, multiplicación y división).
Un quipu, utilizado por los Incas para registrar los números.
Los siguientes avances requirieron la escritura o algún otro sistema para registrar los números, tales como los tallies o las cuerdas anudadas —denominadas quipu —, que eran utilizadas por los Incas para almacenar datos numéricos. Los sistemas de numeración han sido muchos y diversos. Los primeros escritos conocidos que contienen números fueron creados por los egipcios en el Imperio Medio, entre ellos se encuentra el Papiro de Ahmes. La Cultura del valle del Indo desarrolló el moderno sistema decimal, junto con el concepto de cero.
Los antiguos babilonios utilizaban el sistema sexagesimal, escala matemática que tiene por base el número sesenta. De este sistema la humanidad heredó la división actual del tiempo: el día en veinticuatro horas - o en dos períodos de doce horas cada uno -, la hora en sesenta minutos y el minuto en sesenta segundos. Los árabes proporcionaron a la cultura europea su sistema de numeración, que reemplazó a la numeración romana. Este sistema prácticamente no se conocía en Europa antes de que el matemático Leonardo Fibonacci lo introdujera en 1202 en su obra Liber abbaci (Libro del ábaco). En un principio los europeos tardaron en reaccionar, pero hacia finales de la Edad Media habían aceptado el nuevo sistema numérico, cuya sencillez estimuló y alentó el progreso de la ciencia.
Los números mayas del 0 al 19.
Los mayas desarrollaron una avanzada civilización precolombina, con avances notables en la matemática, empleando el concepto del cero, y en la astronomía, calculando con bastante precisión los ciclos celestes.

[editar] Grandes matemáticos de la historia

Algunos de los matemáticos más emblemáticos han sido:
Inventor del Teorema de Tales, que establece que, si a un triángulo cualquiera le trazamos una paralela a cualquiera de sus lados, obtenemos dos triángulos semejantes. Dos triángulos son semejantes si tienen los ángulos iguales y sus lados son proporcionales, es decir, que la igualdad de los cocientes equivale al paralelismo. Este teorema establece así una relación entre el álgebra y la geometría.
  • Pitágoras: (582-500 a. C.). Fundador de la escuela pitagórica, cuyos principios se regían por el amor a la sabiduría, a las matemáticas y música.
Inventor del Teorema de Pitágoras, que establece que, en un triángulo rectángulo, el cuadrado de la hipotenusa (el lado opuesto al ángulo recto) es igual a la suma de los cuadrados de los dos catetos (los dos lados del triángulo menores que la hipotenusa y que conforman el ángulo recto). Además del teorema anteriormente mencionado, también inventó una tabla de multiplicar.
  • Euclides: (aproximadamente 365-300 a. C.). Sabio griego, cuya obra "Elementos de Geometría" está considerada como el texto matemático más importante de la historia.
Los teoremas de Euclides son los que generalmente se aprenden en la escuela moderna. Por citar algunos de los más conocidos:
- La suma de los ángulos interiores de cualquier triángulo es 180°.
- En un triángulo rectángulo el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos, que es el famoso teorema de Pitágoras.
  • Arquímedes: (287-212 a. C.). Fue el matemático más importante de la Edad Antigua. También conocido por una de sus frases: "Eureka, eureka, lo encontré". Su mayor logro fue el descubrimiento de la relación entre la superficie y el volumen de una esfera y el cilindro que la circunscribe. Su principio más conocido fue el Principio de Arquímedes, que consiste en que todo cuerpo sumergido en un fluido experimenta un empuje vertical y hacia arriba igual al peso de fluido que desaloja.
  • Fibonacci: (1170-1240). Matemático italiano que realizó importantísimas aportaciones en los campos matemáticos del álgebra y la teoría de números.Famoso por haber difundido en Europa el sistema de numeración arábiga actualmente utilizado. Descubridor de la Sucesión de Fibonacci, que consiste en una sucesión infinita de números naturales.
  • René Descartes: (1596-1650). Matemático francés, que escribió una obra sobre la teoría de las ecuaciones, en la cual se incluía la regla de los signos, para saber el número de raíces positivas y negativas de una ecuación. Inventó una de las ramas de las matemáticas, la geometría analítica.
  • Isaac Newton: (1643-1727). Matemático inglés, autor de los Philosophiae naturalis principia mathematica. Abordó el teorema del binomio, a partir de los trabajos de John Wallis, y desarrolló un método propio denominado cálculo de fluxiones. Abordó el desarrollo del cálculo a partir de la geometría analítica desarrollando un enfoque geométrico y analítico de las derivadas matemáticas aplicadas sobre curvas definidas a través de ecuaciones.
  • Gottfried Leibniz: (1646-1716). Matemático alemán, desarrolló, con independencia de Newton, el cálculo infinitesimal. Creó la notación y el corpus conceptual del cálculo que se usa en la actualidad. Realizó importantes aportaciones en el campo de la teoría de los números y la geometría analítica.
  • Galileo Galilei: (1564-1642). Matemático italiano, cuyo principal logro fue el crear un nexo de unión entre las matemáticas y la mecánica. Fue el descubridor de la ley de la isocronía de los péndulos. Se inspira en Pitágoras, Platón y Arquímedes y fue contrario a Aristóteles.
  • Blaise Pascal: (1623-1662). Matemático francés que formuló uno de los teoremas básicos de la geometría proyectiva, que se denominó como Teorema de Pascal y que él mismo llamo Teoría matemática de la probabilidad.
  • Leonhard Euler: (1707-1783). Matemático suizo que realizó importantes descubrimientos en el campo del cálculo y la teoría de grafos. También introdujo gran parte de la moderna terminología y notación matemática, particularmente para el área del análisis matemático, como por ejemplo la noción de función matemática.
  • Paolo Ruffini: (1765-1822). Matemático italiano que estableció las bases de la teoría de las transformaciones de ecuaciones, descubrió y formuló la regla del cálculo aproximado de las raíces de las ecuaciones, y su más importante logro, inventó lo que se conoce como Regla de Ruffini, que permite hallar los coeficientes del resultado de la división de un polinomio por el binomio (x - r).
  • Joseph-Louis de Lagrange: (1736-1813). Matemático franco-italiano, considerado como uno de los más importantes de la historia, realizó importantes contribuciones en el campo del cálculo y de la teoría de los números. Fue el padre de la mecánica analítica, a la que dio forma diferencial, creó la disciplina del análisis matemático, abrió nuevos campos de estudio en la teoría de las ecuaciones diferenciales y contribuyó al establecimiento formal del análisis numérico como disciplina.
  • Carl Friedrich Gauss: (1777-1855). Matemático alemán al que se le conoce como "el príncipe de las matemáticas". Ha contribuido notablemente en varias áreas de las matemáticas, en las que destacan la teoría de números, el análisis matemático, la geometría diferencial. Fue el primero en probar rigurosamente el Teorema Fundamental del Álgebra. Inventó lo que se conoce como Método de Gauss, que lo utilizó para resolver sistemas de tres ecuaciones lineales con tres incógnitas.
  • Pierre-Simon Laplace: (1749-1827). Matemático francés que realizó importantes aportaciones a la teoría de Probabilidades, desarrolló la Ecuación de Laplace,e inventó la Transformada de Laplace, que tiene importantes aplicaciones en la electrónica. Fue un ferviente creedor del Determinismo científico.
  • Augustin Louis Cauchy: (1789-1857). Matemático francés, pionero en el análisis matemático y la teoría de grupos. Ofreció la primera definición formal de función, límite y continuidad. También trabajó la teoría de los determinantes, probabilidad, el cálculo complejo, y las series.
  • Jean-Baptiste Joseph Fourier: (1768-1830). Matemático francés. Estudió la transmisión de calor, desarrollando para ello la Transformada de Fourier; de esta manera, extendió el concepto de función e introdujo una nueva rama dentro de la teoría de las ecuaciones diferenciales.

[editar] Influencia en la astronomía moderna

El astrónomo Tycho Brahe anotó minuciosamente durante largo tiempo observaciones planetarias. Cuando leyó El misterio cosmográfico, quedó impresionado con la percepción matemática y astronómica de Kepler y le invitó a trabajar con él en Benatky, localidad cercana a Praga. Al verse obligado a tener que abandonar Graz debido a la intolerancia religiosa, Kepler aceptó la invitación. Al fallecer Brahe, Kepler le sucedió como matemático imperial de Rodolfo II y analizó las medidas sobre la posición de los planetas. Las medidas del movimiento de Marte, en particular de su movimiento retrógrado, fueron esenciales para que pudiera formular las tres leyes de Kepler sobre el movimiento de los planetas. Posteriormente, estas leyes sirvieron de base a la ley de gravitación universal de Newton.

[editar] Crisis históricas

La matemática ha pasado por tres crisis históricas importantes:[11]
  1. El descubrimiento de la inconmensurabilidad por los griegos, la existencia de los números irracionales que de alguna forma debilitó la filosofía de los pitagóricos.
  2. La aparición del cálculo en el siglo XVII, con el temor de que fuera ilegítimo manejar infinitesimales.
  3. El hallazgo de las antinomias, como la de Russell o la paradoja de Berry a comienzos del siglo XX, que atacaban los mismos cimientos de la materia.

[editar] La inspiración, las matemáticas puras y aplicadas y la estética

Artículo principal: Belleza matemática
Sir Isaac Newton (1643-1727), comparte con Leibniz la autoría del desarrollo del cálculo integral y diferencial.
Las matemáticas surgen cuando hay problemas difíciles en los que intervienen la cantidad, la estructura, el espacio y el cambio de los objetos. Al principio, las matemáticas se encontraban en el comercio, en la medición de los terrenos y, posteriormente, en la astronomía. Actualmente, todas las ciencias aportan problemas que son estudiados por matemáticos, al mismo tiempo que aparecen nuevos problemas dentro de las propias matemáticas. Por ejemplo, el físico Richard Feynman inventó la integral de caminos de la mecánica cuántica, combinando el razonamiento matemático y el enfoque de la física. Hoy la teoría de las cuerdas, una teoría científica en desarrollo que trata de unificar las cuatro fuerzas fundamentales de la física, sigue inspirando a las más modernas matemáticas.[12] Algunas matemáticas solo son relevantes en el área en la que estaban inspiradas y son aplicadas para otros problemas en ese campo. Sin embargo, a menudo las matemáticas inspiradas en un área concreta resultan útiles en muchos ámbitos, y se incluyen dentro de los conceptos matemáticos generales aceptados. El notable hecho de que incluso la matemática más pura habitualmente tiene aplicaciones prácticas es lo que Eugene Wigner ha definido como la irrazonable eficacia de las matemáticas en las Ciencias Naturales.[13]
Como en la mayoría de las áreas de estudio, la explosión de los conocimientos en la era científica ha llevado a la especialización de las matemáticas. Hay una importante distinción entre las matemáticas puras y las matemáticas aplicadas. La mayoría de los matemáticos que se dedican a la investigación se centran únicamente en una de estas áreas y, a veces, la elección se realiza cuando comienzan su licenciatura. Varias áreas de las matemáticas aplicadas se han fusionado con otras áreas tradicionalmente fuera de las matemáticas y se han convertido en disciplinas independientes, como pueden ser la estadística, la investigación de operaciones o la informática.
Aquellos que sienten predilección por las matemáticas, consideran que prevalece un aspecto estético que define a la mayoría de las matemáticas. Muchos matemáticos hablan de la elegancia de la matemática, su intrínseca estética y su belleza interna. En general, uno de sus aspectos más valorados es la simplicidad. Hay belleza en una simple y contundente demostración, como la demostración de Euclides de la existencia de infinitos números primos, y en un elegante análisis numérico que acelera el cálculo, así como en la transformada rápida de Fourier. G. H. Hardy en A Mathematician's Apology (Apología de un matemático) expresó la convicción de que estas consideraciones estéticas son, en sí mismas, suficientes para justificar el estudio de las matemáticas puras.[14] Los matemáticos con frecuencia se esfuerzan por encontrar demostraciones de los teoremas que son especialmente elegantes, el excéntrico matemático Paul Erdős se refiere a este hecho como la búsqueda de pruebas de "El Libro" en el que Dios ha escrito sus demostraciones favoritas.[15] [16] La popularidad de la matemática recreativa es otra señal que nos indica el placer que produce resolver las preguntas matemáticas.

[editar] Notación, lenguaje y rigor

Leonhard Euler. Probablemente el más prolífico matemático de todos los tiempos.
Artículo principal: Notación matemática
La mayor parte de la notación matemática que se utiliza hoy en día no se inventó hasta el siglo XVIII.[17] Antes de eso, las matemáticas eran escritas con palabras, un minucioso proceso que limita el avance matemático. En el siglo XVIII, Euler, fue responsable de muchas de las notaciones empleadas en la actualidad. La notación moderna hace que las matemáticas sean mucho más fácil para los profesionales, pero para los principiantes resulta complicada. La notación reduce las matemáticas al máximo, hace que algunos símbolos contengan una gran cantidad de información. Al igual que la notación musical, la notación matemática moderna tiene una sintaxis estricta y codifica la información que sería difícil de escribir de otra manera.
El símbolo de infinito en diferentes tipografías.
El lenguaje matemático también puede ser difícil para los principiantes. Palabras tales como o y sólo tiene significados más precisos que en lenguaje cotidiano. Además, palabras como abierto y cuerpo tienen significados matemáticos muy concretos. La jerga matemática, o lenguaje matematico, incluye términos técnicos como homeomorfismo o integrabilidad. La razón que explica la necesidad de utilizar la notación y la jerga es que el lenguaje matemático requiere más precisión que el lenguaje cotidiano. Los matemáticos se refieren a esta precisión en el lenguaje y en la lógica como el "rigor".
El rigor es una condición indispensable que debe tener una demostración matemática. Los matemáticos quieren que sus teoremas a partir de los axiomas sigan un razonamiento sistemático. Esto sirve para evitar teoremas erróneos, basados en intuiciones falibles, que se han dado varias veces en la historia de esta ciencia.[18] El nivel de rigor previsto en las matemáticas ha variado con el tiempo: los griegos buscaban argumentos detallados, pero en tiempos de Isaac Newton los métodos empleados eran menos rigurosos. Los problemas inherentes de las definiciones que Newton utilizaba dieron lugar a un resurgimiento de un análisis cuidadoso y a las demostraciones oficiales del siglo XIX. Ahora, los matemáticos continúan apoyándose entre ellos mediante demostraciones asistidas por ordenador.[19]
Un axioma se interpreta tradicionalmente como una "verdad evidente", pero esta concepción es problemática. En el ámbito formal, un axioma no es más que una cadena de símbolos, que tiene un significado intrínseco sólo en el contexto de todas las fórmulas derivadas de un sistema axiomático.

[editar] La matemática como ciencia

Carl Friedrich Gauss, apodado el "príncipe de los matemáticos", se refería a la matemática como "la reina de las ciencias".
Carl Friedrich Gauss se refería a la matemática como "la reina de las ciencias".[20] Tanto en el latín original Scientiarum Regina, así como en alemán Königin der Wissenschaften, la palabra ciencia debe ser interpretada como (campo de) conocimiento. Si se considera que la ciencia es el estudio del mundo físico, entonces las matemáticas, o por lo menos matemáticas puras, no son una ciencia.
Muchos filósofos creen que las matemáticas no son experimentalmente falseables, y, por tanto, no es una ciencia según la definición de Karl Popper.[21] No obstante, en la década de 1930 una importante labor en la lógica matemática demuestra que las matemáticas no puede reducirse a la lógica, y Karl Popper llegó a la conclusión de que "la mayoría de las teorías matemáticas son, como las de física y biología, hipotético-deductivas. Por lo tanto, las matemáticas puras se han vuelto más cercanas a las ciencias naturales cuyas hipótesis son conjeturas, así ha sido hasta ahora".[22] Otros pensadores, en particular Imre Lakatos, han solicitado una versión de Falsacionismo para las propias matemáticas.
Una visión alternativa es que determinados campos científicos (como la física teórica) son matemáticas con axiomas que pretenden corresponder a la realidad. De hecho, el físico teórico, J. M. Ziman, propone que la ciencia es conocimiento público y, por tanto, incluye a las matemáticas.[23] En cualquier caso, las matemáticas tienen mucho en común con muchos campos de las ciencias físicas, especialmente la exploración de las consecuencias lógicas de las hipótesis. La intuición y la experimentación también desempeñan un papel importante en la formulación de conjeturas en las matemáticas y las otras ciencias. Las matemáticas experimentales siguen ganando representación dentro de las matemáticas. El cálculo y simulación están jugando un papel cada vez mayor tanto en las ciencias como en las matemáticas, atenuando la objeción de que las matemáticas se sirven del método científico. En 2002 Stephen Wolfram sostiene, en su libro Un nuevo tipo de ciencia, que la matemática computacional merece ser explorada empíricamente como un campo científico.
Las opiniones de los matemáticos sobre este asunto son muy variadas. Muchos matemáticos consideran que llamar a su campo ciencia es minimizar la importancia de su perfil estético, además supone negar su historia dentro de las siete artes liberales. Otros consideran que hacer caso omiso de su conexión con las ciencias supone ignorar la evidente conexión entre las matemáticas y sus aplicaciones en la ciencia y la ingeniería, que ha impulsado considerablemente el desarrollo de las matemáticas. Otro asunto de debate, que guarda cierta relación con el anterior, es si la matemática fue creada (como el arte) o descubierta (como la ciencia). Este es uno de los muchos temas de incumbencia de la filosofía de las matemáticas.
Los premios matemáticos se mantienen generalmente separados de sus equivalentes en la ciencia. El más prestigioso premio dentro de las matemáticas es la Medalla Fields,[24] [25] fue instaurado en 1936 y se concede cada 4 años. A menudo se le considera el equivalente del Premio Nobel para la ciencia. Otros premios son el Premio Wolf en matemática, creado en 1978, que reconoce el logro en vida de los matemáticos, y el Premio Abel, otro gran premio internacional, que se introdujo en 2003. Estos dos últimos se conceden por un excelente trabajo, que puede ser una investigación innovadora o la solución de un problema pendiente en un campo determinado. Una famosa lista de esos 23 problemas sin resolver, denominada los "Problemas de Hilbert", fue recopilada en 1900 por el matemático alemán David Hilbert. Esta lista ha alcanzado gran popularidad entre los matemáticos y, al menos, nueve de los problemas ya han sido resueltos. Una nueva lista de siete problemas fundamentales, titulada "Problemas del milenio", se publicó en 2000. La solución de cada uno de los problemas será recompensada con 1 millón de dólares. Curiosamente, tan solo uno (la Hipótesis de Riemann) aparece en ambas listas.

[editar] Ramas de estudio de las matemáticas

La Sociedad Americana de Matemáticas distingue unas 5.000 ramas distintas de matemáticas.[26] Dichas ramas están muy interrelacionadas. En una subdivisión amplia de las matemáticas, se distinguen cuatro objetos de estudio básicos: la cantidad, la estructura, el espacio y el cambio.
  • Los diferentes tipos de cantidades (números) han jugado un papel obvio e importante en todos los aspectos cuantitativos y cualitativos del desarrollo de la cultura, la ciencia y la tecnología.
  • El estudio de la estructura comienza al considerar las diferentes propiedades de los números, inicialmente los números naturales y los números enteros. Las reglas que dirigen las operaciones aritméticas se estudian en el álgebra elemental, y las propiedades más profundas de los números enteros se estudian en la teoría de números. Después, la organización de conocimientos elementales produjo los sistemas axiomáticos (teorías), permitiendo el descubrimiento de conceptos estructurales que en la actualidad dominan esta ciencia (e.g. estructuras categóricas). La investigación de métodos para resolver ecuaciones lleva al campo del álgebra abstracta. El importante concepto de vector, generalizado a espacio vectorial, es estudiado en el álgebra lineal y pertenece a las dos ramas de la estructura y el espacio.
  • El estudio del espacio origina la geometría, primero la geometría euclídea y luego la trigonometría. En su faceta avanzada el surgimiento de la topología da la necesaria y correcta manera de pensar acerca de las nociones de cercanía y continuidad de nuestras concepciones espaciales.
Derivada.
  • La comprensión y descripción del cambio en variables mensurables es el tema central de las ciencias naturales y del cálculo. Para resolver problemas que se dirigen en forma natural a relaciones entre una cantidad y su tasa de cambio, se estudian las ecuaciones diferenciales y de sus soluciones. Los números usados para representar las cantidades continuas son los números reales. Para estudiar los procesos de cambio se utiliza el concepto de función matemática. Los conceptos de derivada e integral, introducidos por Newton y Leibniz, representan un papel clave en este estudio, que se denomina Análisis. Es conveniente para muchos fines introducir los números complejos, lo que da lugar al análisis complejo. El análisis funcional consiste en estudiar problemas cuya incógnita es una función, pensándola como un punto de un espacio funcional abstracto.
Un campo importante en matemática aplicada es el de la estadística, que permite la descripción, el análisis de probabilidad y la predicción de fenómenos que tienen variables aleatorias y que se usan en todas las ciencias.
El análisis numérico investiga los métodos para realizar los cálculos en computadoras.
A continuación se muestra una lista de las ramas interrelacionadas de las matemáticas:
Fundamentos y métodos
Teoría de conjuntos, lógica matemática, teoría de categorías.
Investigación operativa
Teoría de grafos, teoría de juegos, programación entera, programación lineal, Simulación, optimización, método simplex, programación dinámica.
Números
Números naturales, números enteros, números racionales, números irracionales, número reales, números complejos, cuaterniones, octoniones, sedeniones, números hiperreales, números infinitos, dígito, sistema de numeración, número p-ádico.
Análisis, continuidad y cambio
Cálculo, cálculo vectorial, análisis, ecuaciones diferenciales, sistemas dinámicos y teoría del caos, funciones, logaritmo, sucesiones, series, análisis real, Análisis complejo, análisis funcional, álgebra de operadores.
Estructuras
Algebra abstracta, teoría de números, álgebra conmutativa, geometría algebraica, teoría de grupos, monoides, análisis, topología, álgebra lineal, teoría de grafos, teoría de categorías.
Espacios
Topología, geometría, teoría de haces, geometría algebraica - Geometría diferencial - Topología diferencial - Topología algebraica - Álgebra lineal - Cuaterniones y rotación en el espacio
Matemática discreta
Combinatoria, Teoría de conjuntos numerables - Probabilidad discreta - Estadística - Teoría de la computación - Criptografía - Teoría de grafos - Teoría de juegos
Matemática aplicada
Estadística, física matemática, matemática financiera, teoría de juegos, optimización, análisis numérico, Lógica difusa.

[editar] Conceptos erróneos

Lo que cuenta como conocimiento en matemática no se determina mediante experimentación, sino mediante demostraciones. No es la matemática, por lo tanto, una rama de la física (la ciencia con la que históricamente se encuentra más emparentada), puesto que la física es una ciencia empírica. Por otro lado, la experimentación desempeña un papel importante en la formulación de conjeturas razonables, por lo que no se excluye a ésta de la investigación en matemáticas.
La matemática no es un sistema intelectualmente cerrado, donde todo ya esté hecho. Aún existen gran cantidad de problemas esperando solución, así como una infinidad esperando su formulación.
Matemática no significa contabilidad. Si bien los cálculos aritméticos son importantes para los contables, los avances en matemática abstracta difícilmente cambiarán su forma de llevar los libros.
Matemática no significa numerología. La numerología es una pseudociencia que utiliza la aritmética modular para pasar de nombres y fechas a números a los que se les atribuye emociones o significados esotéricos, basados en la intuición.
El lenguaje formal no es una simple extensión de los lenguajes naturales humanos que utiliza una gramática y un vocabulario definidos con extrema precisión, cuyo propósito es la descripción y exploración de relaciones conceptuales y físicas. Recientemente, los avances en el estudio del lenguaje humano apuntan en una dirección diferente: los lenguajes naturales (como el español o el francés, por ejemplo) y los lenguajes formales (como el matemático o los lenguajes de programación) son estructuras de naturaleza básicamente diferente.

[editar] Véase también

[editar] Referencias

  1. ↑ En la antigüedad nadie hizo un retrato o una descripción de la apariencia física de Euclides mientras estaba vivo. Por lo tanto, la representación de Euclides en las obras de arte varía en función de la imaginación de cada artista (véase Euclides).
  2. ↑ «matemática», Diccionario de la lengua española (vigésima segunda edición), Real Academia Española, 2001, http://buscon.rae.es/draeI/SrvltConsulta?TIPO_BUS=3&LEMA=matem%C3%A1tica 
  3. ↑ Steen, LA (29 de abril de 1988). Mathematics:The Science of Patterns (Scientific American Library, 1994) Science, 240: 611-616.
  4. ↑ Matemáticas: La ciencia de los patrones: La búsqueda de la Orden en la vida, la mente y el Universo. Scientific American. ISBN 9780716750475. 
  5. ↑ Jourdain
  6. ↑ Peirce, p.97
  7. ↑ Einstein, p. 15. La cita es la respuesta de Einstein a la pregunta: "¿Cómo puede ser que las matemáticas, siendo después de todo un producto del pensamiento humano independiente de la experiencia, estén tan admirablemente adaptadas a los objetos de la realidad? [1]"
  8. ↑ Peterson
  9. ↑ Heath, Thomas (1921). A History of Greek Mathematics.. Oxford, Clarendon Press. OCLC 2014918. 
  10. ↑ S. Dehaene, Dehaene-Lambertz G. y L. Cohen, Resumen de los números de las representaciones en el cerebro humano y animal,Tendencias en Neurociencias, vol. 21 (8), agosto de 1998, 355-361. http://dx.doi.org/10.1016/S0166-2236 (98) 01263-6.
  11. ↑ El dedo de Galileo. Peter Atkins. En Espasa Calpe-2003
  12. ↑ Johnson, Gerald W.; Lapidus, Michel L. (2002). Oxford University Press. ed. The Feynman Integral and Feynman's Operational Calculus. 
  13. ↑ Eugene Wigner, 1960, "La irracional eficacia de las matemáticas en la de Ciencias Exactas y Naturales" Communications on Pure and Applied Mathematics13 '(1): 1-14.
  14. ↑ Hardy, GH (1940). A Mathematician's Apology. 
  15. ↑ Oro, Bonnie; Simons, A. Rogers (2008). MAA. ed. Proof and Other Dilemmas: Mathematics and Philosophy. 
  16. ↑ Aigner, Martin; Ziegler, M. Gunter (2001). Proofs from the Book. 
  17. ↑ Utilización de diversos símbolos matemáticos (Véase Anexo:Símbolos matemáticos)
  18. ↑ Véase falsa demostración para comprobar mediante ejemplos sencillos los errores que se pueden cometer en una demostración oficial. El teorema de los cuatro colores contiene ejemplos de demostraciones falsas aceptadas accidentalmente por otros matemáticos del momento.
  19. ↑ Ivars Peterson,La matemática turística, Freeman, 1988, ISBN 0-7167-1953-3. p. 4 "Algunos se quejan de que el programa de ordenador no puede ser verificado correctamente," (en referencia a la Haken de Apple la prueba de color Teorema de los Cuatro).
  20. ↑ Waltershausen
  21. ↑ Shasha, Dennis Elliot; Lazere, Cathy A. (1998). Fuera de su mente: La vida y de 15 de los Grandes Descubrimientos científicos. p. 228. 
  22. ↑ Popper 1995, p. 56
  23. ↑ Ziman
  24. ↑ «Actualmente la Medalla Fields es sin duda el mejor y el más influyente premio en las matemáticas». Monastyrsky
  25. ↑ Riehm
  26. ↑ Clasificación bibliográfica de la Sociedad Americana de Matemáticas de 2010

[editar] Bibliografía

[editar] Enlaces externos

Wikilibros
Il logo di Wikisource Conosci Wikisource, la biblioteca libera? - Guarda la breve video-guida su Wikisource prodotta da Wikimedia Italia Il logo di Wikimedia

Teorema di Pitagora

Da Wikipedia, l'enciclopedia libera.
Vai a: navigazione, cerca
La somma delle aree dei due quadrati costruiti sui cateti (blu e rosso) è equivalente all'area del quadrato costruito sull'ipotenusa (viola).
Il teorema di Pitagora è un teorema della geometria euclidea che stabilisce una relazione fondamentale tra i lati di un triangolo rettangolo ed è una versione limitata ad essi del Teorema di Carnot.

Indice

[nascondi]

[modifica] Origine

Visualizzazione del caso del triangolo (3,4,5) contenuta nel testo cinese Chou Pei Suan Ching (scritto tra il 200 a.C. e il 200 d.C.)
Quello che modernamente conosciamo come teorema di Pitagora viene solitamente attribuito al filosofo e matematico Pitagora. In realtà il suo enunciato (ma non la sua dimostrazione) era già noto[1] ai babilonesi, ed era conosciuto anche in Cina e forse in India. La dimostrazione del teorema è invece con ogni probabilità successiva a Pitagora.

[modifica] Enunciato

In ogni triangolo rettangolo, l'area del quadrato costruito sull'ipotenusa è equivalente alla somma delle aree dei quadrati costruiti sui cateti.
Rtriangle.svg
Dato un triangolo rettangolo di lati a, b e c, ed indicando con c la sua ipotenusa e con a e b i suoi cateti, il teorema è espresso dall'equazione:
a^2 + b^2 = c^2\,
o, in alternativa, risolvendolo per c:
\sqrt{a^2 + b^2} = c. \,
Da cui si ricavano i rispettivi cateti:

\sqrt{c^2 - b^2} = a. \,
e
\sqrt{c^2 - a^2} = b. \,
Se la terna a,b,c è costituita da numeri interi essa si chiama terna pitagorica.
Inversamente, ogni triangolo in cui i tre lati verificano questa proprietà è rettangolo: questo teorema, con la sua dimostrazione, appare negli Elementi immediatamente dopo il teorema di Pitagora stesso.

[modifica] Dimostrazioni

Animazione di una dimostrazione
La dimostrazione classica del teorema di Pitagora completa il primo libro degli Elementi di Euclide, e ne costituisce il filo conduttore. Dato che richiede il postulato delle parallele, esso non vale nelle geometrie non-euclidee e nella geometria neutrale. Nel testo di Euclide la dimostrazione del teorema è immediatamente preceduta dalla dimostrazione della costruibilità dei quadrati. L'esistenza stessa dei quadrati dipende infatti dal postulato delle parallele e viene meno nelle geometrie non euclidee. Questo aspetto del problema è in genere trascurato nella didattica contemporanea, che tende spesso ad assumere come ovvia l'esistenza dei quadrati.
La dimostrazione del teorema di Pitagora consiste nel riempire uno stesso quadrato di lato uguale alla somma dei cateti prima con quattro copie del triangolo rettangolo più il quadrato costruito sull'ipotenusa e poi con quattro copie del triangolo rettangolo più i quadrati costruiti sui cateti, come in figura.
Dimostrazione di Perigal
Essendo il teorema uno dei più noti della storia della matematica, ne esistono moltissime dimostrazioni, in totale alcune centinaia, opera di matematici, astronomi, agenti di cambio, per esempio un presidente americano James A. Garfield e Leonardo da Vinci. Questo numero così alto accomuna il teorema di Pitagora a quello della reciprocità quadratica, per questo teorema sono state classificate dallo scienziato americano Elisha Scott Loomis 371 differenti dimostrazioni, che sono state pubblicate nel 1927 nel suo libro The Pythagorean Proposition.

[modifica] Dimostrazione di Perigal

Esaminiamone alcune interessanti. Quella proposta nel 1873 dall'agente di cambio Henry Perigal si basa sulla scomposizione del quadrato costruito sul cateto maggiore, in giallo nell'immagine: tagliandolo infatti con due rette passanti per il suo centro, una perpendicolare ed una parallela all'ipotenusa, si può ricomporre in maniera da incorporare l'altro quadrato, e formando il quadrato sull'ipotenusa, come nella figura.

[modifica] Dimostrazione di Airy

Dimostrazione di Airy
Esiste anche una dimostrazione in forma poetica, dell'astronomo Sir George Airy, in inglese:
"I am, as you can see, a² + b² - ab When two triangles on me stand, Square of hypothenuse is plann'd But if I stand on them instead The squares of both sides are read."
di cui una traduzione letterale è
"Come potete vedere, sono a² + b² - ab Quando ci sono due triangoli sopra di me È rappresentato il quadrato dell'ipotenusa Ma se invece sto io sopra di loro Si leggono i quadrati dei due lati"
I versi si riferiscono alla parte bianca: i primi due triangoli sono quelli rossi, i secondi quelli blu.
Sia quella di Perigal che quest'ultima sono interessanti, in quanto sono puramente geometriche, ossia non richiedono alcuna definizione di operazioni aritmetiche, ma solo congruenze di aree e di segmenti.

[modifica] Quadrati concentrici di Pomi

Dimostrazione con quadrati concentrici
Dimostrazione geometrica basata su due quadrati concentrici, di lati rispettivamente pari all'ipotenusa (c) e alla somma dei due cateti (a+b).
Come si vede dalla figura, tolti i 4 triangoli rettangoli (in giallo di area (a * b) / 2) al quadrato più grande, che corrisponde all'area (a + b)2, si ottiene il quadrato più piccolo, rappresentato in bianco, che equivale invece all'area c2.
Quindi (a + b)2 − 4 * (a * b) / 2 = c2
da sui risolvendo si ottiene : a2 + b2 = c2
Questa dimostrazione ha il vantaggio di avere una rappresentazione visiva semplice e diretta, che non richiede lo spostamento e sovrapposizione di forme come le altre dimostrazioni geometriche formulate.

[modifica] Dimostrazione di Garfield

Dimostrazione di Garfield
Un'altra dimostrazione geometrica particolarmente significativa, in quanto nella costruzione non compare alcun quadrato, fu trovata nel 1876 da Garfield, che in seguito divenne il ventesimo Presidente degli Stati Uniti d'America. Allora nell'esercito, Garfield commentò il suo risultato: "Questo è qualcosa su cui i due rami del parlamento potranno essere d'accordo".
La dimostrazione è la seguente:
consideriamo una copia del triangolo rettangolo in questione, ruotata di 90 gradi in modo da allineare i due cateti differenti (nella figura a lato il rosso ed il blu). Si uniscono poi gli estremi delle ipotenuse, e si ottiene un trapezio. Uguagliando l'area del trapezio alla somma di quelle dei tre triangoli retti, si dimostra il teorema.
In formule, detto a il cateto rosso, b il blu e c l'ipotenusa, e ricordando la potenza del binomio
\frac {(a+b)^2} 2 = \frac {{ab}} 2 + \frac {{ab}} 2 + \frac {c^2} 2 \,\, \Rarr \,\, a^2 + b^2 = c^2

[modifica] Una apparente dimostrazione con i numeri complessi

Una (apparente) dimostrazione puramente algebrica fa uso dei numeri complessi e della formula di Eulero: siano a, b i cateti e c l'ipotenusa. Se i cateti sono allineati sugli assi, abbiamo
a + ib = ceiθ
Consideriamo ora il complesso coniugato di a + ib:
a − ib = ce − iθ
Moltiplicando tra loro otteniamo
a2 + b2 = c2
In realtà si tratta di una dimostrazione apparente, poiché il risultato è supposto implicitamente nell'uso dell'identità eiθe − iθ = 1 .
Se infatti si sostituisce all'esponenziale immaginario la sua definizione, l'identità si rivela essere: (cosθ + isenθ)(cosθ − isenθ) = 1, ossia cos2θ + sen2θ = 1
e l'ultima ben nota identità non è altro che una possibile formulazione dell'enunciato del teorema di Pitagora.
(Se invece l'esponenziale immaginario è definito attraverso la somma della sua serie di Taylor, allora il problema diviene quello di dimostrare la relazione a + ib = ceiθ, dove a, b e c sono le misure di cateti e ipotenusa di un triangolo rettangolo: problema la cui soluzione di nuovo non è più semplice di una delle dimostrazioni precedenti del teorema di Pitagora).

[modifica] Con i teoremi di Euclide

Dimostrazione con Euclide
Un'altra dimostrazione utilizza il primo teorema di Euclide. Si traccia l'altezza sull'ipotenusa, di lunghezza h. Questa spezza l'ipotenusa in due segmenti, di lunghezza p e q. Il teorema di Euclide fornisce le relazioni
\frac ap = \frac ca, \ \frac bq = \frac cb,
da cui
a^2 = cp, \ b^2 = cq
e quindi
a^2 + b^2 = c(p+q) = c^2.\,\!

[modifica] Inverso

Vale anche l'inverso del Teorema di Pitagora (proposizione 48 del primo libro degli Elementi di Euclide): "Se in un triangolo di lati a, b e c vale la relazione a2 + b2 = c2, allora il triangolo è rettangolo".
Dimostrazione. Sia T un triangolo di lati a, b e c tale che a2 + b2 = c2. Consideriamo un secondo triangolo rettangolo T' che abbia i cateti pari ad a e b (è sempre possibile costruire un triangolo rettangolo dati i due cateti). Per il Teorema di Pitagora (diretto) l'ipotenusa del triangolo T' sarà pari a 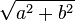\sqrt{a^2 + b^2}, ossia sarà uguale al lato c del triangolo T. I due triangoli T e T' risulteranno dunque congruenti per il terzo criterio di congruenza, avendo tutti e tre i lati ordinatamente uguali. Ma allora anche il triangolo T sarà rettangolo (CVD).

[modifica] Applicazioni pratiche dell'enunciato inverso

L'enunciato inverso fornisce anche un semplicissimo sistema per costruire un angolo retto (o per controllare la quadratura di un angolo già esistente) in situazioni pratiche, come la topografia o l'agrimensura.
A titolo di esempio, con una fune di lunghezza pari alla somma di una terna pitagorica (diciamo 12, somma di 5, 4 e 3, in una qualche unità di misura) sarebbe sufficiente disporre le due porzioni minori della corda (quelle di misura 4 e 3) ad un certo angolo fra loro; se gli estremi della fune, disposta infine in forma triangolare, si chiudono, si saprà che l'angolo compreso fra le due porzioni minori della corda (a questo punto i due cateti) è certamente retto.

[modifica] Generalizzazioni

Il teorema di Pitagora può essere generalizzato in vari modi. Solitamente, una generalizzazione è una relazione che si applica a tutti i triangoli, e che applicata ai triangoli rettangoli risulta essere equivalente al teorema di Pitagora.

[modifica] Teorema del coseno

Un triangolo qualsiasi.
Exquisite-kfind.png Per approfondire, vedi la voce Teorema del coseno.
La generalizzazione più importante del teorema di Pitagora è forse il teorema del coseno, che si applica ad un triangolo qualsiasi (non necessariamente retto). In un triangolo con vertici e angoli indicati come in figura, vale l'uguaglianza:
\overline{AB}^2=\overline{AC}^2+\overline{BC}^2-2\overline{AC}\cdot\overline{BC}\cos\gamma.
Nel caso in cui γ sia retto, vale cosγ = 0 e quindi l'enunciato è equivalente al teorema di Pitagora. Il termine aggiuntivo può essere interpretato come il prodotto scalare dei vettori CA e CB.

[modifica] Teorema dei seni

Exquisite-kfind.png Per approfondire, vedi la voce Teorema dei seni.
Il teorema dei seni mette in relazione lunghezze dei lati e angoli opposti.
Il teorema dei seni mette in relazione le lunghezze dei lati di un triangolo e i seni degli angoli opposti. Anche questa relazione si applica a qualsiasi triangolo e, nel caso in cui questo sia rettangolo, può essere ritenuta equivalente al teorema di Pitagora (benché in modo meno immediato rispetto al teorema del coseno).
Il teorema dei seni asserisce che in un triangolo qualsiasi, con le notazioni come in figura, valgono le relazioni seguenti:
\frac a{\sin\alpha}=\frac b{\sin\beta}=\frac c{\sin\gamma}=2R.
Elevando al quadrato:
c^2= a^2\frac {\sin^2\gamma}{\sin^2\alpha}, \quad b^2= a^2 \frac{\sin^2\beta}{\sin^2\alpha}.
Sommando i termini si ottiene:
c^2 + b^2 =a^2\frac {\sin^2\gamma + \sin^2\beta}{\sin^2\alpha}.
Quando α è un angolo retto, si ottiene β = π / 2 − γ e quindi
\frac {\sin^2\gamma + \sin^2\beta}{\sin^2\alpha} = \sin^2(\pi/2-\beta) + \sin^2\beta = \cos^2\beta + \sin^2\beta = 1.
Si ottiene quindi in questo caso il teorema di Pitagora
c^2 + b^2 = a^2.\,\!

[modifica] Generalizzazione che non fa uso di trigonometria

Generalizzazione del teorema di Pitagora.
È possibile estendere il teorema di Pitagora ad un triangolo qualsiasi senza fare uso di funzioni trigonometriche quali il seno ed il coseno. Dato un triangolo ABC come in figura, si tracciano due segmenti che collegano il vertice A con due punti g e h contenuti nel segmento opposto BC (oppure in un suo prolungamento), in modo tale che gli angoli AgB e AhC siano entrambi uguali all'angolo α del vertice A. La figura mostra un caso in cui l'angolo α è ottuso: se è acuto, i due punti g e h sono in ordine inverso (il primo a destra e il secondo a sinistra) e possono uscire dal segmento BC.
Vale la relazione seguente:
\overline {AB}^2 + \overline{AC}^2 = \overline {BC}\cdot (\overline{Bg} + \overline{hC}).
Quando α è un angolo retto, i punti g e h coincidono e si ottiene il teorema di Pitagora
\overline {AB}^2 + \overline{AC}^2 = \overline {BC}\cdot (\overline{Bg} + \overline{hC}) = \overline{BC}^2.
La relazione generale può essere dimostrata sfruttando la similitudine fra i triangoli ABC, gBA e hAC, che porta alle relazioni
\frac{\overline{AB}}{\overline{BC}}=\frac{\overline{Bg}}{\overline{AB}},\quad \frac{\overline{AC}}{\overline{BC}}=\frac{\overline{hC}}{\overline{AC}}.
Si ottiene quindi
\overline{AB}^2 = \overline{BC}\cdot \overline{Bg}, \quad \overline{AC}^2 = \overline{BC}\cdot \overline{hC}.
Sommando le due eguaglianze si ottiene la relazione iniziale.

[modifica] Leggenda di Pitagora e delle piastrelle

Rappresentazione grafica del teorema.
Una leggenda racconta che Pitagora abbia formulato il suo teorema mentre stava aspettando un'udienza da Policrate. Seduto in un grande salone del palazzo di Samo, Pitagora si mise ad osservare le piastrelle quadrate del pavimento, si pensa che ne abbia vista una rotta perfettamente su di una diagonale, così da formare due triangoli rettangoli uguali, ma oltre ad essere 2 triangoli rettangoli erano anche isosceli, avendo i due lati uguali. Pitagora immaginò un quadrato costruito sulla diagonale di rottura della piastrella, un quadrato avente come lati le diagonali delle piastrelle circostanti.
La dimostrazione è la seguente:
  • l'area di ogni lato era di: 2 mezze piastrelle,
  • la somma delle due aree era di: 4 mezze piastrelle,
  • l'area del quadrato costruito sull'ipotenusa (diagonale della piastrella) era di: 4 mezze piastrelle.[2]

[modifica] Note

  1. ^ Viene a volte affermato che il teorema di Pitagora fosse noto agli antichi Egizi. Carl B. Boyer esclude questa ipotesi, basandosi sull'assenza del teorema dai papiri matematici rinvenuti. Si veda l'opera di Boyer citata in bibliografia, a pag. 20 dell'edizione italiana.
  2. ^ Leggenda di Pitagora e delle piastrelle di Policrate

[modifica] Bibliografia

[modifica] Voci correlate

[modifica] Altri progetti

[modifica] Collegamenti esterni


matematica Portale Matematica: accedi alle voci di Wikipedia che trattano di matematica

Estratto da "http://it.wikipedia.org/wiki/Teorema_di_Pitagora"
Strumenti personali
Namespace
Varianti
Azioni
Ultima modifica pe
Publicado por en

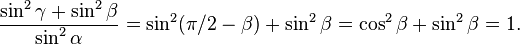
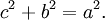
No hay comentarios:

Publicar un comentario

Suscribirse a: Enviar comentarios (Atom)